Tensors

?? What are tensors? ????

Tensors are fundamental mathematical objects used to describe various physical properties, similar to scalars and vectors. In fact, tensors are an extension of scalars and vectors, where a scalar represents a zero-rank tensor, and a vector represents a first-rank tensor.

The rank or order of a tensor is determined by the number of directions required to describe it, which also determines the dimensionality of the tensor array. For instance, a first-rank tensor (1D) can be fully described by a 3×1 column vector, while a second-rank tensor (2D) requires nine numbers arranged in a 3×3 matrix. In general, an nth rank tensor can be represented by 3n coefficients.

The necessity for second rank tensors arises when multiple directions are needed to describe certain physical properties. An illustrative example is the description of electrical conductivity in a general, anisotropic crystal. For isotropic conductors following Ohm's law, conductivity can be expressed as:

j = σE

Let's explore different types of tensors:

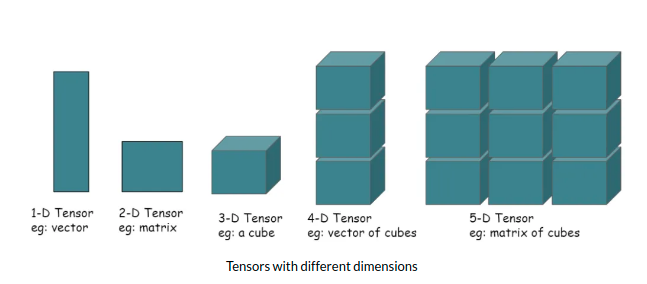
0D Tensors/Scalars:?

A tensor with zero dimensions is known as a 0D tensor or scalar. For example, (2) or (3) can be considered as 0D tensors. In practical terms, we can represent a 0D tensor using the following code:

import numpy as np?

a = np.array(2)

print(a.ndim)

Output:0

1D Tensors/Vectors:

A tensor with one dimension is referred to as a 1D tensor or vector. For example, [1, 2, 3, 4] can be considered a 1D tensor. In practical terms, we can represent a 1D tensor using the following code:

import numpy as np

a = np.array([1, 2, 3, 4])

print(a.ndim)

Output: 1

The dimension of the vector depends on the number of elements in the array.

2D Tensors/Matrices:

A collection of multiple vectors forms a 2D tensor, also known as a matrix. For example, if we have [1, 2, 3], [4, 5, 6], and [7, 8, 9], combining these vectors creates a 2D tensor. In practical terms, we can represent a 2D tensor using the following code:

import numpy as np?

a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

print(a.ndim)

Output: 2

3D Tensors:?

A three-dimensional array can be referred to as a 3D tensor. A 3D tensor is also known as a cube. Here is an example code representing a 3D tensor:

import numpy as np?

x = np.array([[[56, 183, 1],?

[65, 164, 0]],?

[[85, 176, 1],?

[44, 164, 0]]])

The dimensions of the tensor x are (2, 3, 3), indicating a rank of 3. To access elements like 56, 176, or 44, you would use the respective indices: x[0][0][0], x[1][0][1], x[1][1][0]. As each number requires three indices for access, the rank of the tensor is 3.

4D Tensors:

?A vector of 3D tensors is called a 4D tensor. 4D tensors are often used in image analysis. Here's a practical example:

import numpy as np?

tensor_4D = np.array([[[[0, 1, 1],?

[2, 3, 3],

[1, 3, 2]],?

[[1, 3, 2],?

[2, 4, 2],?

[0, 1, 1]]],?

[[[0, 3, 1],?

[2, 4, 1],?

[1, 3, 2]],?

[[1, 1, 1],?

[2, 3, 4],?

[1, 3, 2]]],?

[[[2, 2, 4],?

[2, 1, 3],?

[0, 4, 2]],?

[[2, 4, 1],?

[2, 3, 0],?

[1, 3, 3]]]])?

print("Tensor dimensions: \n{}".format(tensor_4D.ndim))

Output: Tensor dimensions: 4

5D Tensors:

A matrix of 4D tensors is referred to as a 5D tensor. 5D tensors find their application in video data analysis. Let's consider an example of a 5-minute video with 1080 HD resolution. In this case, the data structure dimension can be calculated as follows: The pixel size is 1080 x 1920 pixels, and the video duration in seconds is 5 x 60 = 300 seconds. If the video is sampled at 10 frames/second, the total number of frames will be 300 x 10 = 3000. Assuming the video has a color depth of 3, the tensor representing this video should have 4 dimensions, with a shape of (3000, 1080, 1920, 3).

Therefore, a single video clip can be represented as a 4D tensor. If we want to store multiple videos, such as 10 video clips with 1080 HD resolution, we would need a 5D tensor. The shape of this 5D tensor would be (3000, 1080, 1920, 3, 10).

Conclusion:

• A tensor can be thought of as a data container, similar to a multi-dimensional array.
• Numpy's np.array can be used to create tensors of different dimensions, such as 1D, 2D, 3D, etc.
• A vector is a 1D tensor, and a matrix is a 2D tensor. A 0D tensor is a scalar or a numerical value.
• Accessing a specific value in a tensor is also called tensor slicing.
• Two key attributes of tensors are: A. Rank or axes of the tensor B. Shape of the tensor

By using ndim and shape on a Numpy array, you can determine the rank and shape of the tensor, respectively.

#Tensors #DataScience #MachineLearning #DeepLearning #TensorAnalysis

#artificialintelligence