Interpreting Regression Coefficients

I’ve been doing regressions for years now and I made numerous mistakes in understanding regression coefficients. I was surprised to see these mistakes being made in published papers and reports. This blog is a primer on how to correctly interpret these coefficients.

I created a dummy data, purely for educational purposes. I’ll tell the math behind the dummy data at the end. My dummy data consists of 200 people — 100 from India (80 Hindus — 20 Muslims), 100 from Pakistan (80 Muslims — 20 Hindus). The response variable (y) is Happiness score for each of them. This is how the dataset looks like.

Both Religion and Country are predictors (Xs) and they are binary variables. Hindu = 1, Muslim = 0; India = 1, Pakistan = 0.

I ran two regressions and created a poll on LinkedIn asking data analysts for their interpretations.

a) ?????????????????? = 5.95 + 3.55*(??????????)

b) ?????????????????? = 4.73–0.09*(??????????) + 6.07*(??????????)

[The 0.09 coefficient is not statistically significant. All other coefficients are statistically significant]

Not many responded to the poll, but these were its results:

Lets see who were wrong as we interpret the regression coefficients.

0. Regression with a Constant = 1

We regress the response variable with a constant variable of value 1.

#Regress with constant
y = df.Happiness
df['c'] = 1
X = df[['c']]

results = sm.OLS(y, sm.add_constant(X)).fit()
print(results.summary())        

Which is exactly equal to the mean happiness of all the 200 people in my dummy dataset.

If the constant is not equal to 1, the coefficient will be divided by that constant. Basically the mulitple of constant and coefficient will be the mean of the response variable.

Interpretation: When we regress the response variable (y) with a constant (c = 1), the regression coefficient is just the mean of the response variable.

1. Simple Linear Regression (one predictor)

We’d rarely regress a response variable with a constant. Simple Linear Regression is what we’d generally start our regression journey with.

Let’s regress Happiness (y) of people with the religion they belong to.

y = df.Happiness
X = df[['Religion']]

results = sm.OLS(y, sm.add_constant(X)).fit()
print(results.summary())        

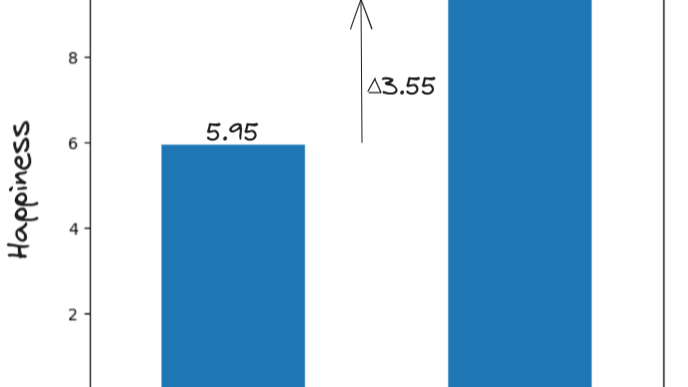
This is the first regression result I shared in the poll. It basically says:

?????????????????? = 5.95 + 3.55*(Religion)

The coefficient says that Hindus 3.55 points more happier than Muslims, on an average (in this data). But regression coefficients only tell correlation — not causation. The coefficient value does not mean that Hinduism is the reason for their Happiness. There could be other reasons as well and a data analyst should check for them.

Nevertheless, on an average, Hindus are 3.55 points happier. You can observe it visually when you plot it.

4/9 voters interpreted it right.

Interpretation: When we regress the response variable (y) with a single predictor (x), the regression coefficient is just the comparison of the average.

2. Multiple Linear Regression (more predictors)

As I mentioned above, a diligent data analyst should check for other reasons as well. In our dataset, we have another predictor variable — Country. Let’s add that to the mix.

y = df.Happiness
X = df[['Religion', 'Country']]

results = sm.OLS(y, sm.add_constant(X)).fit()
print(results.summary())        

?????????????????? = 4.73–0.09*(Religion) + 6.07*(Country)

Suddenly, the coefficient of Religion became neglible (and statistically insignificant — ‘0’ coefficient value falls within the confidence interval). And 5/9 voters interpreted this to mean that Religion has zero effect on Happiness. What they mean is that people are happy because of the country they live in and not because of the religion per se. The large positive coefficient to Country variable, makes their interpretation right. Indians are happier than Pakistanis, and since more Hindus are in India, their average Happiness score is also higher.

Here’s the twist in the tale. The 5/9 voters are wrong.

Because, I manufactured religious discrimination in the dummy dataset. Here’s how I did it:

For Indians, I gave a mean happiness of 10 points with 1 standard deviation. But I then added 1 point to every Hindu.

india = np.append(np.ones(80), np.zeros(20))

#Mean=10; SD=1
india_happiness = np.random.normal(10,1,100) 

india_df = pd.DataFrame([india,india_happiness]).T
india_df.columns = ['Religion', 'Happiness']
india_df['Country'] = 1

#Add one point to every Hindu (Religion=1)
india_df.loc[india_df['Religion'] == 1, 'Happiness'] += 1        

For Pakistanis, I gave a mean happiness of 5 points with 0.5 standard deviation. But I then removed 1 point to every Hindu.

pakistan = np.append(np.ones(20), np.zeros(80))

#Mean=5; SD=0.5
pakistan_happiness = np.random.normal(5,0.5,100)

pak_df = pd.DataFrame([pakistan,pakistan_happiness]).T
pak_df.columns = ['Religion', 'Happiness']
pak_df['Country'] = 0
#Reduce one point to every Hindu (Religion=1)
pak_df.loc[pak_df['Religion'] == 1, 'Happiness'] -= 1        

So I manufactured majoritarianism in my dummy dataset. Majority religion is happier, but the average happiness levels varied in both countries.

Why did the regression coefficient for Religion then become negligible?

Also note: had I not added that religious discrimination to Happiness, my regression equation would be similar to the negligible coefficient to Religion. Then, these 5/9 voters’ interpretation would’ve been right. Why are they not wrong in this case?

Let me interpret it right:

Interpretation: In Multiple Linear Regression, Regression Coefficient is the average of the slopes between the response (y) and predictor (x) possible with combinations of all other predictors (X-x)

We are interpreting the coefficient of the predictor Religion (x). And we have one another predictor Country. There are two slopes (two combinations) possible here:

1. Slope between Happiness and Religion in India (b1)
2. Slope between Happiness and Religion in Pakistan (b2)

And the regression coefficient is the average of these slopes. I’ll show it visually.

(b1+b2)/2 = (0.7306–0.9165)/2 = -0.0929! (The negligible regression coefficient in the equation)

The regression coefficient is thus averaging the advantage the majority religion have in one country and the disadvantage they have in another. To interpret it to mean that Religion has no effect on Happiness is wrong.

So, we should be able to tease out these slopes to tell the truth. ‘Interaction variables’ is a tool that helps in bringing out this truth.

Interaction variable

So, we add another variable to the regression mix. It is just the product of the Religion and Country.

y = df.Happiness
df['ReligionXCountry'] = df['Religion']*df['Country']
X = df[['Religion', 'Country', 'ReligionXCountry']]

results = sm.OLS(y, sm.add_constant(X)).fit()
print(results.summary())        

?????????????????? = 4.73–0.92*(Religion) + 5.25*(Country) + 1.65*(Religion*Country)

So, when we speak about India, substitute Country = 1 and the above equation becomes

?????????????????? = 4.73–0.92*(Religion) + 5.25*(1) + 1.65*(Religion*1)

?????????????????? = 9.98 + 0.73*(Religion)

b1 = 0.73 !!

When we speak about Pakistan, substitute Country = 0 and the above equation becomes

?????????????????? = 4.73–0.92*(Religion) + 5.25*(0) + 1.65*(Religion*0)

?????????????????? = 4.73–0.92*(Religion)

b2 = -0.92 !!

For the sake of explanation and visualisation I have considered all my predictors to be binary. But the interpretations remain the same even if they are discrete or continuous.

Interaction variables are important especially when the relationship between the response (y) and a predictor (x) can change from positive to negative, in relation ot another variable. If I can assume that all slopes are positive or negative, then the average of slopes makes sense. It gives us the average relation between the predictor and response. But if this assumption cannot hod, the average masks the truth.