Grokking: A Deep Dive into Delayed Generalization in Neural Networks

The world of deep learning is full of mysteries. One of the most intriguing is the phenomenon of grokking, where neural networks exhibit surprisingly delayed generalization, achieving high performance on unseen data long after they have seemingly overfit their training set. This behavior defies conventional machine learning wisdom, prompting researchers to delve deeper into its origins and implications.

This blog post explores the fascinating world of grokking, drawing insights from two groundbreaking papers: "Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets" by Power et al. and "Towards Understanding Grokking: An Effective Theory of Representation Learning" by Liu et al. We'll unravel the key concepts, delve into the mathematical underpinnings, and uncover the potential implications of this intriguing phenomenon.

The Grokking Puzzle:

Imagine training a neural network on a simple task, like learning the addition operation. You'd expect the network to quickly memorize the training examples and then generalize to unseen additions. However, in grokking, the network overfits the training data, achieving near-perfect accuracy, but struggles to generalize to new examples for a surprisingly long time. Only after extensive training does it suddenly "grok" the underlying pattern and achieve perfect generalization.

This behavior raises several fundamental questions:

• Q1: The Origin of Generalization: How do neural networks generalize at all when trained on these algorithmic datasets?
• Q2: The Critical Training Size: Why does the training time required to "grok" diverge as the training set size decreases?
• Q3: Delayed Generalization: What conditions lead to this delayed generalization?

Unraveling the Mystery:

The research suggests that representation learning is the key to understanding grokking. This means that the network learns to represent the input data in a way that captures the underlying structure of the task. This structured representation, rather than mere memorization, enables generalization.

Effective Theories and Representation Dynamics :

Liu et al propose an effective theory to explain the dynamics of representation learning in a simplified toy model. This theory, inspired by physics, provides a simplified yet insightful picture of how the network learns to represent the data.

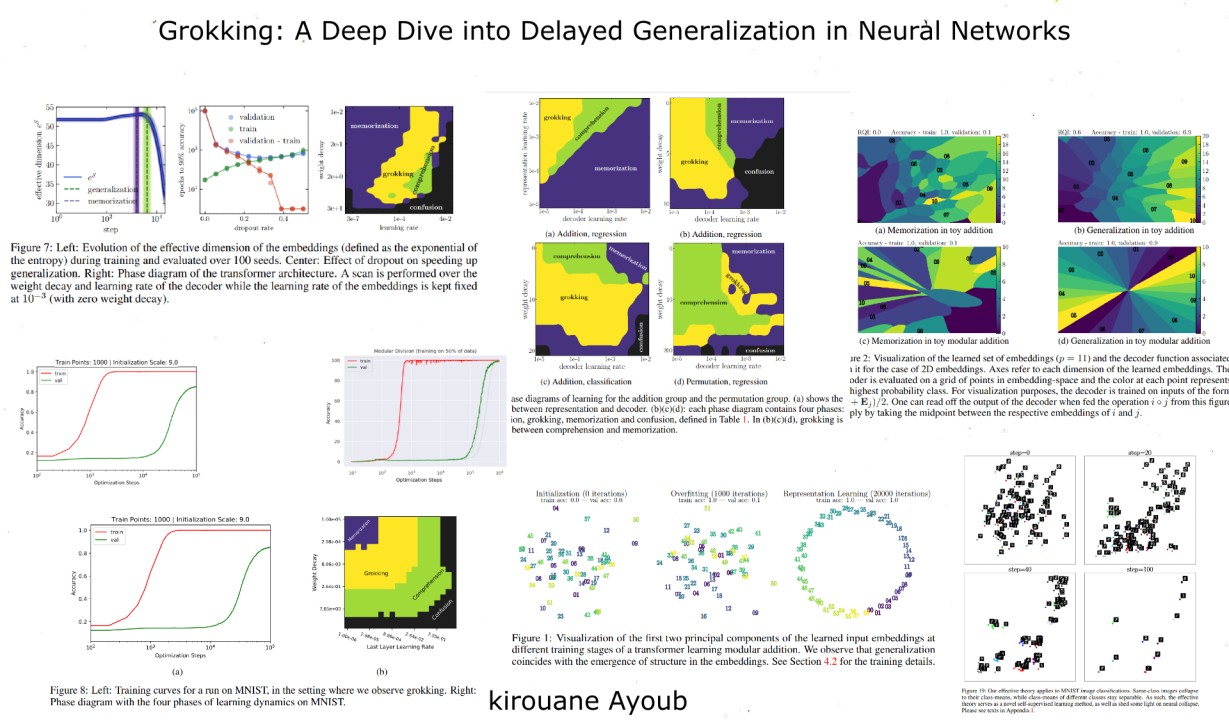
The Toy Model: The model learns the addition operation by mapping input symbols to trainable embedding vectors. These vectors are then summed and passed through a decoder network. The key insight is that generalization occurs when the embedding vectors form a structured representation, specifically parallelograms in the case of addition.

Representation Quality Index (RQI): This index quantifies the quality of the learned representation by measuring the number of parallelograms formed in the embedding space. A higher RQI indicates a more structured representation, leading to better generalization.

Effective Loss Function: The effective theory proposes a simplified loss function that captures the dynamics of representation learning. This loss function encourages the formation of parallelograms, driving the network towards a structured representation.

Grokking Rate: The effective theory also predicts a "grokking rate," which determines the speed at which the network learns the structured representation. This rate is inversely proportional to the training time required for generalization.

Critical Training Size: The effective theory predicts a critical training set size below which the network fails to learn a structured representation and thus fails to generalize. This explains why the training time diverges as the training set size decreases.

Phase Diagrams and Learning Phases :

Liu et al. further explore the learning dynamics by constructing phase diagrams that map the learning performance across different hyperparameter settings. These diagrams reveal four distinct learning phases:

• Comprehension: The network quickly learns a structured representation and generalizes well.
• Grokking: The network overfits the training data but generalizes slowly, exhibiting delayed generalization.
• Memorization: The network overfits the training data and fails to generalize.
• Confusion: The network fails to even memorize the training data.

The phase diagrams show that grokking occurs in a "Goldilocks zone" between memorization and confusion. This zone represents a delicate balance between the capacity of the decoder network and the speed of representation learning.

Beyond the Toy Model: Grokking in Transformers and MNIST

The insights gained from the toy model extend to more complex architectures, such as transformers.

Power et al demonstrate grokking in transformers trained on modular addition, observing that generalization coincides with the emergence of circular structure in the embedding space.

Liu et al further show that grokking can be observed even on mainstream benchmark datasets like MNIST. By carefully adjusting the training set size and weight initialization, they induce grokking in a simple MLP. This suggests that grokking is a more general phenomenon than previously thought.

De-Grokking: Mitigating Delayed Generalization

By carefully tuning hyperparameters, such as weight decay and learning rates, we can shift the learning dynamics away from the grokking phase and towards comprehension. This involves finding the right balance between representation learning and decoder capacity.

Weight Decay: Weight decay, a common regularization technique, plays a crucial role in de-grokking. By adding weight decay to the decoder, we effectively reduce its capacity, preventing it from overfitting the training data too quickly. This allows the representation learning process to catch up and form a structured representation that enables generalization. Liu et al. [2] demonstrate that applying weight decay to the decoder in transformers can significantly reduce generalization time and even eliminate the grokking phenomenon altogether.

Learning Rates: The learning rates for both the representation and the decoder also influence the learning dynamics. A faster representation learning rate can help the network discover the underlying structure more quickly, while a slower decoder learning rate can prevent it from overfitting too rapidly. Finding the right balance between these learning rates is crucial for achieving comprehension and avoiding grokking.

Implications and Future Directions :

The discovery of grokking has significant implications for our understanding of deep learning:

Generalization Beyond Memorization: Grokking challenges the traditional view of generalization as simply memorizing training data. It highlights the importance of learning structured representations that capture the underlying patterns of the task.

The Role of Optimization: Grokking emphasizes the crucial role of optimization in shaping the learning dynamics and influencing generalization.

New Insights into Representation Learning: Grokking provides a unique lens for studying representation learning, offering a quantitative measure of representation quality and insights into the dynamics of representation formation.

Future research directions include:

• Exploring Grokking in Other Domains: Investigating grokking in other domains, such as natural language processing and computer vision, to understand its generality and potential applications.
• Developing More Powerful Effective Theories: Refining the effective theory to capture more complex learning dynamics and provide more accurate predictions.
• Understanding the Role of Implicit Regularization: Investigating the role of implicit regularization, such as weight decay and dropout, in shaping the learning dynamics and influencing grokking.
• Connecting Grokking to Other Phenomena: Exploring the connections between grokking and other deep learning phenomena, such as double descent and neural collapse.

Conclusion: A New Frontier in Deep Learning

Grokking is a fascinating phenomenon that challenges our understanding of deep learning. By delving into its origins and implications, we gain valuable insights into the nature of generalization, the importance of representation learning, and the power of optimization. As we continue to explore this intriguing phenomenon, we unlock new frontiers in deep learning, paving the way for more powerful, efficient, and interpretable models.

References:

Power, Alethea, et al. "Grokking: Generalization beyond overfitting on small algorithmic datasets." arXiv preprint arXiv:2201.02177 (2022).

Liu, Ziming, et al. "Towards Understanding Grokking: An Effective Theory of Representation Learning." arXiv preprint arXiv:2205.10343 (2022).

• Kirouane Ayoub