Embedding Entire Graphs or Sub-Graphs: Part 7 of X of my notes
Ajay Taneja
Senior Data Engineer | Generative AI Engineer at Jaguar Land Rover | Ex - Rolls-Royce | Data Engineering, Data Science, Finite Element Methods Development, Stress Analysis, Fatigue and Fracture Mechanics
1. Introduction:
?
This is the continuation of my series of blogs on Graphs and is the 7th blog in the series. In my last two articles, I have been talking of node embeddings – the article 5 [https://www.dhirubhai.net/pulse/understanding-node-embeddings-graphs-part-5-x-my-notes-ajay-taneja-1f0jf/?trackingId=MeSAsXW%2BT4CiGzGcbCzOog%3D%3D ] emphasized on the concept of “Graph Representation Learning” wherein rather than extracting node level, link level, graph level features using manual feature engineering, the idea was that given each node we map each node into a d-dimensional embedding space. These node embeddings in the d-dimensional embedding space capture the underlying graph network we’re interested in. The goal of the node embeddings is to encode the nodes so that the similarity in the embedding space is approximated by similarity in the graph?– so that similar nodes lie close to one another in the embedding space.
?
The article 6 [https://www.dhirubhai.net/pulse/formulation-node-embeddings-graphs-node2vec-algorithm-ajay-taneja-trndf/?trackingId=MeSAsXW%2BT4CiGzGcbCzOog%3D%3D ], then, went into the formulation of Node Embeddings using the Node2Vec algorithm. The article highlighted some very important concepts in Graphs such as “context” of the Graphs which the node embeddings attempt to emulate as discussed in section 3 of my sixth article. The article re-visited the skip gram model used to generate word embeddings in natural language processing and then went onto explain how the same skip gram model could be well used for generating node embeddings in a Graph thus highlighting the conceptual similarity between word and node embeddings.
?
This article will talk about embedding entire graphs. That is: rather than embedding individual nodes, how do we go about embedding the entire graph or a sub-graph within a graph? We will be discussing 4 approaches that may be used for embedding entire graphs:
The above are discussed through the following sections in this article. Generally speaking, one may want to embed entire graphs or sub-graphs into an embedding space for different use cases:
?
?
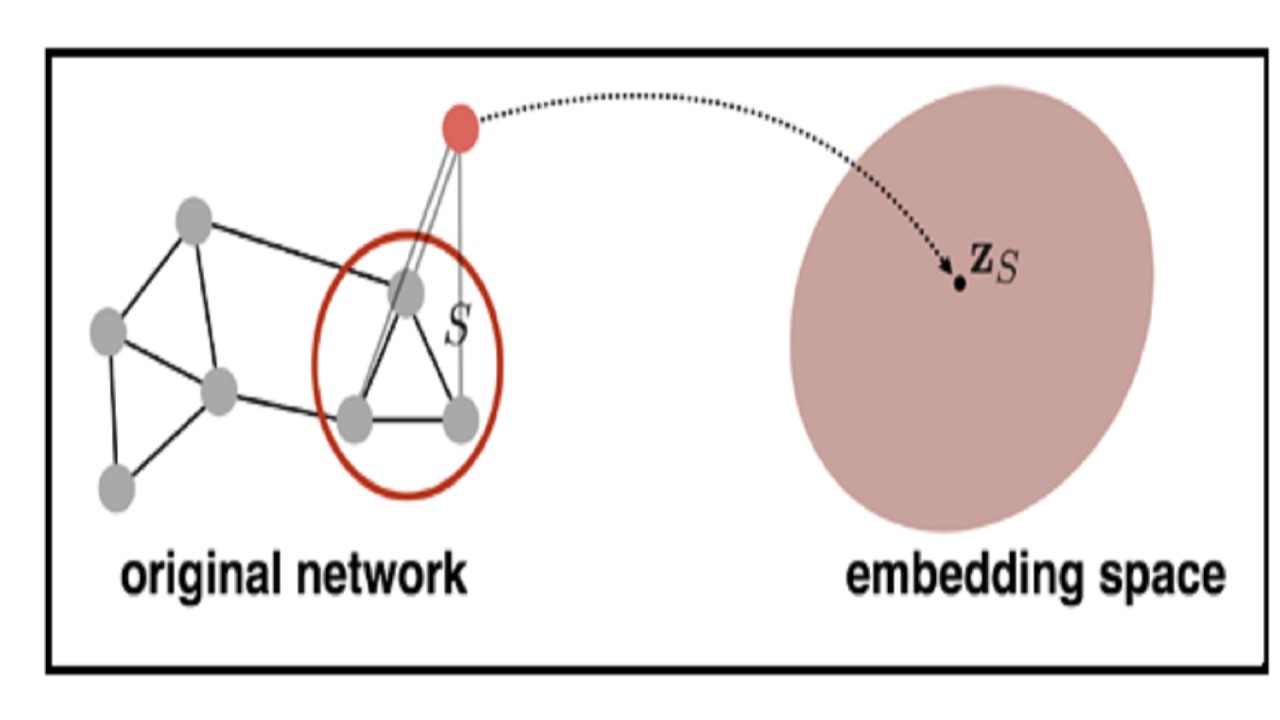
The goal is then to embed the entire graph into an embedding space or a sub-set of nodes in the graph into an embedding space as shown in the figure below:
There could be different approaches to do this and let us now discuss some of these different approaches and these are discussed in the sections below.
2. Embedding entire graphs as the sum of node embeddings:
In this approach, one runs the standard technique of embedding individual nodes as already discussed in the part 6 of my ongoing series of blogs on graphs here using the Node2Vec algorithm. Following this, to get the embedding of the entire graph, one averages the node embeddings of the entire graph or sub-graph as represented in the equation below:
This method was used in 2016 by Duvenud et all in their 2016 paper titled: “Convolutional Networks on Graphs for Learning Molecular Fingerprints ” for classification of molecules based on the graph structure and it was very successful. It was a very simplistic approach and the authors quoted of it working very well in practice.
3. Embedding graphs through a virtual node:
?
An improvement over the initial idea of averaging the node embeddings is to introduce a virtual node to represent the entire graph or sub-graph and then run a standard node embedding technique like Node2Vec. The virtual node – as shown in the figure below – essentially represents the embedding for the entire graph.
The overall steps in this approach may be explained as follows:
If one wants to embed the entire graph, then, the virtual node will connect to all the nodes in the network. This approach was proposed by Li et all and is elaborated in the paper titled “Gated Graph Sequence Neural Networks” available here .
4. Embedding graphs through Anonymous Random Walks:
This approach was published in the paper “Anonymous Walk Embeddings” by Sergey Ivanoc and Ergeny Burnaer [https://arxiv.org/abs/1805.11921 ]. This paper was published in 2018 and was another approach to embed entire graphs.
I have attempted to explain the concept involving obtaining the Graph Embeddings through Anonymous Walks through the following sub-sections:
?
?
Overall idea of embedding entire graphs using Anonymous Walk Embeddings:
Fundamentally speaking, we want to embed the entire graph into the embedding space. To be able to successfully, embed the graph one should be able to encapsulate the “context” of the entire graph. The “context” of the graph comes through:
?
?
I had talked about the concepts related to Breadth First Search (BFS) and Depth First Search (DFS) in the part 6 of this series of blog in section 3 ?here . To get the immediate neighbours of a node and its connections through the depth of a graph, one has to run random walks taking each node.
?
Aggregating probabilities across all vertices in a graph and normalizing them by the total number of nodes we get the probability of choosing anonymous walk ai in the graph G. And this is what “Anonymous Random Walks” will aim to do as explained in the subsequent paragraphs.
What are the Anonymous Walks?
?
Let us consider an example sub-graph of interest – for which we might be wanting to generate the embedding – shown in the figure below:
Let us say, that, we’re doing a random walk starting at A and then traverse to B and then to C and then come back to B and then move to C as shown in the figure below.
Another Random walk which starts at C goes to D and then to B to D and back to B as shown below:
Or another Random walk as shown below:
领英推荐
In Anonymous random walks, we’re not going to represent the random walks by the sequence of node labels but by the sequence of time step indices when the node was visited as shown below. Hence, they are called “Anonymous Random Walks”.
Why Anonymous Random Walks?
It should be underscored that if a node was already visited during the random walk and gets visited again, it does not get a new index but gets assigned the same index value as shown in the Figure 6/7/8/9 above.
As one may notice, with anonymous walks, the random walks across the same sub-graph are essentially the same considering the indices rather than the node labels which helps the in the subsequent steps of generating node embeddings (Random Walk 1 and Random Walk 2 of represented in Figure 6 and Figure 7). Thus, using the concept of Anonymous Random Walks, it is possible to ascertain if a walk has already been visited.
When dealing with Random walks across networks like social media network, then, since the network is private, it is not possible to know the entire topology of the network relating to node labels, connections, etc. In such scenarios, in order to carry out the random walks, it would be the best to do the walks anonymously as described in the above paragraphs.
?
?
Number of possible anonymous random walks across a graph:
Number of possible anonymous random walks across a graph or a sub-graph increase exponentially across the length of the graph. For example, for a length of 3, there are 5 possible random walks – considering that there are no constraints as shown below.
The 5 possible random walks of length 3 include:
W1 = 111 – here you start at the same node 3 times
W2 = 112 – here you stay at the same node at the first and he second time step and then move to the second node.
W3 = 121 – Here you go from the first node to the second and then back to the first.
Similarly, we have the random walks:
W4 = 1 2 2
And
W5 = 1 2 3
The number of possible Random walks increase exponentially with length, and this is highlighted in the figure below:
5. How do we embed graphs through Random walks of length l?
?
To simulate Random Walks of length l, the idea is to simulate the random walks of length l and represent the graph as a probability distribution over these walks.
Since the number of random walks increase exponentially with increase in the length of the graph as discussed in the preceding section and illustrated in Figure 10, one needs to have an idea about the number of random walks that must be sampled to capture the context of the graph such that the error is negligible.
The paper gives an idea of how many random walks “m” one would want to sample such that the estimate and the probability of occurrence is accurate. The paper states that one can quantify the accuracy by 2 parameters: ε and δ where we say that we want the distribution of the probabilities of random walks to have an error of no more than ε with probability less than δ.
The resulting equation for the total number of random walks is given by:
Where:
η = total number of anonymous random walks of length l
?
For example,
There are η = 877 anonymous random walks of length l = 7. If we set, ε = 0.1 and δ = 0.01.
From the above, we would generate m = 122,500 random walks to arrive at a probability of error less than 0.01
As it may be observed, when a random walk is expressed in form of indices, then one can identify if the context of that sub-graph is already been accounted for.
An anonymous walk is a high-level representation of all the random walk probabilities starting from node u. Aggregating probabilities across all vertices in a graph and normalizing them by the total number of nodes we get the probability of choosing anonymous walk ai in the graph G.
?
6. Learning Walk Embeddings
?
The idea behind random walks can further be enhanced by learning the embeddings of the walks. That is:
?
The embeddings pf the entire graph will correspond to the embedding obtained as the concatenation of all the random walks from each node of the graph that make the overall context of the graph.
?
So, the total number of walk embeddings that will have to be learnt be total number of anonymous walks plus 1 – the additional one for the embedding of the graph.
?
How to embed walks?
This is done in a very similar way to what it was done for Node2Vec – here we want to embed walks than embedding nodes.
For example, starting from node 1 in the graph, we have sample random walks as shown below:
The idea is to learn to predict walks that co-occur in some ? - size window on which we sample the random walks from a given node. This is again the same as we predict the contextual words in a sentence in word2vec and generate the embeddings as weights in the hidden layer.
?
The objective function is the same as used in skip gram model in the Word2Vec or Node2Vec as discussed here .
Thus: